Physics - Intro to Projectile Motion Continues

LEARNING OBJECTIVES:

1. Recall/practice with the relationship between the hypotenuse and the sides of a right triangle using trig.
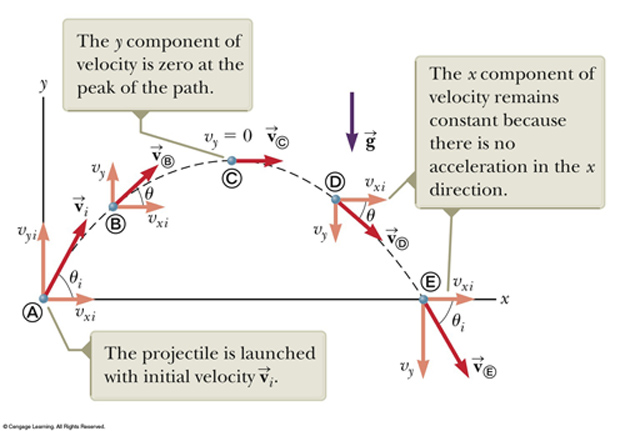
2. Objects in projectile motion have zero acceleration in X (horizontal)

CALENDAR:

WORDS O' THE DAY:

• Projectile Motion - Up/Vertical (y motion) AND Out/Horizontal (x motion)

FORMULAE OBJECTUS:

1a) v_fx = v_ix +a_xt

1a) v_fy = v_iy +a_gt

2a) x_f = x_i + v_it + 1/2at²

2b) y_f = y_i + v_it + 1/2a_gt²

3a) v_f² - v_i² = 2a∆x

3b) v_f² - v_i² = 2a_g∆y

WORK O' THE DAY:

What do we mean by the term "Projectile Motion?"

Please discuss with your team upwards (y or vertical motion) AND outwards (x or horizontal motion) at the same time.

Those two motions are intricately linked together:

What percentage of that object's motion is horizontal at h_max?

What percentage of that object's motion is vertical at h_max?

Compare the motion of the object at Points A & E.

Yeah... but what does it MEAN?

═══════════════════════════

Let's do a wee bit o' practice with vectors again before we dig in:

If we kick a ball with an initial velocity of 12.45 m/s at an angle of 29.5 degrees to the horizontal, what is the ball's vertical velocity?

What is the ball's horizontal velocity?

If we shoot a grape with our trusty wrist rocket with an initial velocity of 32.2 m/s at an angle of 41 degrees to the horizontal, what is the ball's vertical velocity?

What is the ball's horizontal velocity?

═══════════════════════════

You are out golfing with your (omnipotent) friend. You blast the ball as hard as you can and your omnipotent friend immediately determines the horizontal velocity as

v_ix =28.23 m/s

and a total flight time of 3.99 seconds.

How far away did the ball hit the ground (if we ignore friction and the usual noes)?

We use a particularly simple formulae to calculate horizontal (X) displacement, why is that?

ANSWER: (Sweep your mouse →) The formula x = (v_ix)(t) is used to calculate JUST the horizontal motion. Horizontal motion is independent of gravity if we ignore friction (which we are doing in this problem).

Now please finish that calculation.

 

ANSWER: (Sweep your mouse →) x = (v_ix)(t) so x = (28.23 m/s)(3.99 s) = 112.6 m => 113 m s.f.

Now you're curious what your initial velocity was... and of course your friend has perfect, instant recall and tells you that your golf club hit the ball at an angle of 27.3 degrees to the horizontal.

HUH? "Hey omnipotent friend!" (you say) "I asked you to tell me the initial velocity and you gave me the launch angle instead. What gives?"

Your (not-so-gracious-OR-humble) friend smirks and replies:

"I gave you plenty of information, now YOU figure it out."

So... do that now (please).

Hint (Sweep your mouse →): List all initial conditions

Hint(2) (Sweep your mouse →): Don't forget the definition of cosine

═══════════════════════════

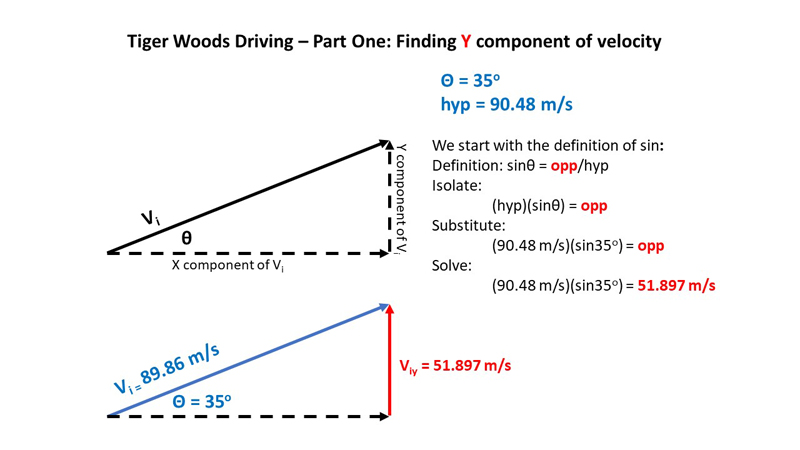
Rumor has it that the "perfect" angle to hit a golf ball is at 35^o to the horizontal.

Tiger Woods has hit a golf ball in excess of 200 mph off the tee.

So, let's say Tiger Woods smacks a golf ball at 202.4 mph at an angle 35^o to the horizontal:

Please address each question in a full sentence response:

• What do we mean by "to the horizontal?"
• Does the golf ball move faster or slower after it has left Tiger's golf club?

Now let's HIT the work!

• Sketch that situation showing the initial velocity (magnitude AND direction please) in meters/sec if you please!
• Now calculate the initial velocity in the Y (vertical) direction (v_iy)
• Now please calculate how high the ball will go (h_max)
• Now please calculate how long it will take to get to h_max
• What is the vertical component of the golf ball's velocity at h_max?
• Now please determine how long it will take for the golf ball to fall back to the ground
• How long was that ball in flight?

═══════════════════════════

═══════════════════════════

WHEW! That's a fair bit of work!

But now we know how long the ball is in flight we can do the X (horizontal) calculations lickety split.... by doing.... what, exactly? Please discuss.

 

 

══════════════════════════════